Factor de Carga: Ejercicio Propuesto

En esta oportunidad, tocaremos el tema del factor de carga, uno de los tantos tópicos fascinantes del mundo aeronáutico. Además, te ayudaré a visualizar desde su importancia hasta su aplicación de manera analítica. Comencemos:

¿Qué es el factor de carga?

 El factor de carga puede definirse como la relación que existe entre la fuerza total que actúa sobre un avión y el peso del mismo, se denota con la letra "n" y se suele expresar en Gs (una unidad de aceleración que representa la aceleración gravitacional en la superficie terrestre) aunque es una magnitud adimensional. En otras palabras, cualquier fuerza aplicada a una aeronave para desviar su vuelo de una trayectoria de línea recta produce un esfuerzo sobre su estructura, la relación de dicha fuerza con respecto al peso de la aeronave no es más que el factor de carga.

Supongamos que nuestra aeronave con un peso de 19600 N realiza una maniobra en la que todas las fuerzas actuantes sobre ella alcanzan los 24000 N. Mediante la siguiente ecuación, podríamos conocer el factor de carga con respecto a dicha maniobra:

n = (fuerzas que actúan sobre el avión) / (peso del avión)

n = (24000 N)/ 19600 N = 1.22

Esto quiere decir que la aeronave está soportando 1.22 veces su peso mientras ejecuta la maniobra.

En algunos casos, la ecuación puede arrojarnos un resultado en el que "n" quede negativo. Esto ocurre porque el factor de carga no solamente depende de las fuerzas que actúan sobre la aeronave, también depende de la orientación de su eje vertical. Para entenderlo mejor, imaginemos que un avión está en vuelo recto y nivelado, debido a que en este caso la única fuerza actuando sobre la aeronave es la de la sustentación entonces es sencillo determinar que el factor de carga es 1, puesto que la aeronave está sustentando lo que pesa y la dirección del vector sustentación es completamente vertical hacia arriba. Pero, ¿qué pasaría si la aeronave se colocase boca abajo en las mismas circunstancias?, lo que sucedería es que la dirección del vector sustentación pasaría a ser negativa y por lo tanto el factor de carga nos arrojaría un resultado de -1.

Vector sutentación en vuelo recto y nivelado.

Vector sustentación cuando el avión se encuentra volando completamente boca abajo.

¿Para qué sirve?

Una pregunta que probablemente nos hayamos hecho en algún punto es la de: "¿qué tan fuerte debería ser la estructura de una aeronave?", pregunta que por cierto está muy sugestionada a la misión que tenga la misma. Sin embargo, el factor de carga es extremadamente importante para responder la pregunta anteriormente planteada, puesto que nos permite conocer a qué magnitud de cargas se enfrentará dicha aeronave en las maniobras más críticas, y por lo tanto, permite poder diseñar con mayor seguridad.

Generalmente, las aeronaves comerciales suelen tener factores de carga "seguros" los cuales no deben de sobrepasarse bajo ninguna circunstancia ya que ponen en peligro la estructura del avión, esto, ayuda a los pilotos a conocer que maniobras no deben realizar y hasta que punto pueden "forzar" movimientos bruscos. 

Otro aspecto curioso e importante del factor de carga es que incrementa la velocidad en la que una aeronave puede entrar en perdida. Es decir, si una aeronave fue diseñada para que entrase en perdida a una velocidad de 120km/h en vuelo recto y nivelado, entonces esta entrará en perdida incluso antes si realiza una maniobra en la que aumente su factor de carga. Por ejemplo:

Velocidad de entrada en perdida = 120km/h

Pero si se realiza una maniobra en la que n = 2, entonces;  (120km/h)*(raíz cuadrada de n) = 137km/h.

Es importante recalcar que el factor de carga se aplica a todas las maniobras de vuelo. Considerando lo anterior, observemos como se comporta una aeronave al realizar un viraje:

Aeronave realizando un viraje.

Un viraje se caracteriza por aumentar el factor de carga, esto ocurre debido a que la fuerza de la sustentación no se comporta de manera completamente vertical. 

Si tomamos en cuenta todas las fuerzas que actúan en el eje Z y suponemos que la aeronave se encuentra en equilibrio dinámico, tendremos lo siguiente:

(L)(cos&) - w = 0

L = w / cos&

Donde L es la sustentación, & es el angulo de inclinación y w es el peso de la aeronave. Si consideramos que la única fuerza real que afecta a nuestra aeronave es la sustentación, entonces podemos determinar de que: n = L/w

Ejemplo

Una aeronave tiene una magnitud de vuelo en crucero de 0.3 Mach con un peso de 20000 N y un arrastre de crucero "D" de 20000 N. Se asume que el arrastre en la velocidad de crucero es constante y una atmósfera ISA. La aeronave procede a realizar un Looping y se desea encontrar el factor de carga presente en la misma cuando esta se encuentre a 90 grados antes de llegar al punto más alto.  Las condiciones de vuelo en dicha maniobra son: empuje T = 50000 N, un coeficiente de sustentación "CL" de 0.9556 y una velocidad de 0.7 Mach. Encontrar además el radio de giro de la maniobra "Rcg". Considere que la aeronave posee el mismo coeficiente de sustentación mientras se encuentra en vuelo recto y nivelado.

Resolución:

Primeramente, debemos realizar la conversión de 0.3 Mach a metros/seg para que concuerden las unidades más adelante. Considerando que el ejercicio nos indica que la atmósfera es ISA (recordemos que la velocidad del sonido depende de las condiciones atmosféricas en las que se estudia), entonces tenemos que:

Velocidad en crucero = 81.5139 m/seg

Continuando, debemos analizar que está ocurriendo con la aeronave mientras esta se encuentra en vuelo recto y nivelado antes de entrar a analizar la maniobra.

Aeronave en vuelo de crucero

Considerando un equilibrio dinámico, tenemos que:

∑ Fx = 0

T = D

∑ Fz = 0

L = W

Recordemos entonces la ecuación de la sustentación.

L = ½ ρ v² CL Sw 

Procedemos a obtener el valor de la superficie alar "Sw" porque es un valor que necesitaremos en el momento en el que vayamos a calcular la sustentación cuando el avión realice la maniobra.

En una atmosfera ISA,  ρ = 1.225 kg/m³

Sustituyendo:

Sw = (20000 N)(2) /(81,5139)²(1,225 kg/m³)(0.9556)

Sw  = 5.1426 m²

Ya conociendo la superficie alar, podemos empezar a analizar a la aeronave mientras está realizando el Looping.

Velocidad en la maniobra = 206.5324 m/seg

Con la velocidad en la maniobra y con la superficie alar que habíamos obtenido anteriormente, podemos calcular la sustentación mientras se ejecuta la maniobra.

L = (½)(1,225 kg/m³)(0,9556) (206.5234m/seg)²

L = 33349.32 N

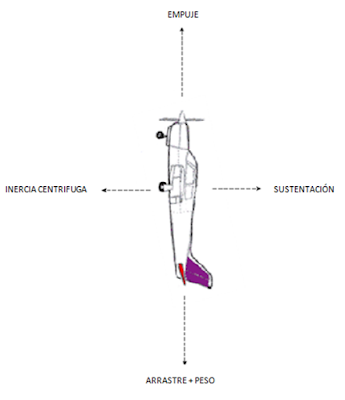Aeronave a 90 grados mientras ejecuta el Looping.

Tomando en cuenta que la única fuerza que actúa sobre la aeronave es la sustentación, tenemos que:

n = L/w

n = (33349.32 N)/(20000 N)

n = 1.66

Para calcular el radio de giro de la aeronave, debemos tomar en cuenta que:

Inercia centrífuga = (V²/Rcg)(w/g)

Considerando lo anterior, realizamos nuevamente la sumatoria de fuerzas en equilibrio dinámico:

∑ Fx = 0

(V²/Rcg)(w/g) + L = 0

Despejamos el radio de giro:

Rcg = (V²)(w)/(L)(g)

Rcg = (206.5234m/seg)²(20000 N) / (33349.52 N) (9.81 m/seg²)

Rcg = 2607.41 metros

A continuación, puedes observar más detalladamente la solución del ejercicio mediante un vídeo explicativo: